√ ニュートン 微分法 209149-ニュートン 微分法

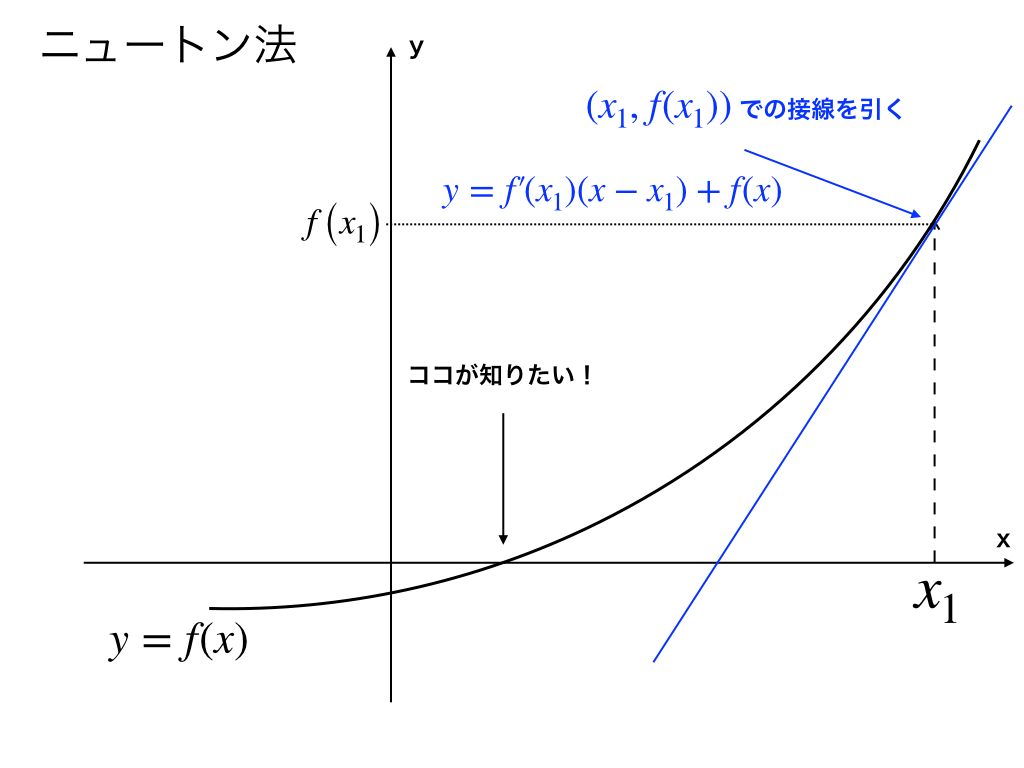
微分法を使って，「y＝x」を微分しよう コラム ニュートンはこんな人 猫専用のドアを発明!?ニュートン法 を使って適当な初期値の元に解け。 微分方程式とルンゲクッタ法 常微分方程式 を解析的解くには となり、境界条件を入れて解けば となる。これは解析解であるがルンゲ・クッタ法を使った数値解は次のように補間関数の形で求まる。 問題 ニュートン法の考え方 ニュートン法では、以下の考え方に基づいて計算が行われます f (x) = 0になるような値xを探す時、ある値x1における接線の切片x2は、元の値x1より真の値xに近くなる この考え方は下の図のように、f (x)という関数においてf (x) = 0になる

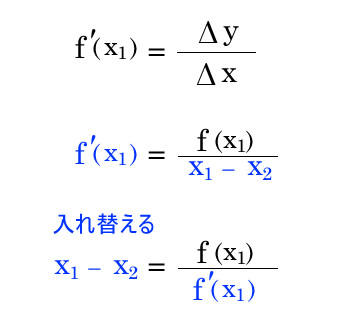
ニュートン法で近似解 Python Numpy 優技録

ニュートン 微分法

ニュートン 微分法-• ある点x nでの導 ニュートン法のプログラム ←割る数が0でないか（小さ過ぎないか）チェック ←x を更新 ← 反復停止条件 演習問題 • 以下の問題について、作成したニュートン法 で解いてみよう。! ニュートン法の解説とそれを背景とする入試問題 レベル ★ 最難関大受験対策 極限，微分 更新日時 ニュートン法 (Newton's method) は，方程式の解を高速に計算するアルゴリズムである。 ニュートン法と呼ばれるアルゴリズムに関連した入試問題

微分積分 運動を語る数学の共通言語 空間情報クラブ 株式会社インフォマティクス

5分でわかる「ニュートンの冷却の法則」理系学生ライターがわかりやすく解説 よぉ、桜木建二だ。 今回は、伝熱学で学習する「ニュートンの冷却の法則」について解説していくぞ。 「ニュートンの冷却の法則」は、熱くなった物体が冷却されていく様子 至急！ニュートン法に関してです！ ニュートン方の式を授業では 1=f'()/f"() （最後の項は二回微分ぶんの一回微分） と習ったのですが いろいろなサイトをみていると 最後の項が f（）/f'()となっています （もとの関数ぶんの一回微分） 授業のプログラミングでも二回微分で行なったニュートン法(ニュートン・ラフソン法) とは︖ 非線形方程式f(x) = 0 を数値的に解く方法の1つ 微分可能な方程式であれば、たとえ微分しなくても解が求まる 繰り返し計算により解に近づく 初期値を変えて何回か解く方がよい 1 問題設定 2 非線形方程式f (x) = 0 の解x を求める 曲線y = f (x) におけ

 非正則な複素関数のニュートン法 複素関数 f(z) が非正則（複素微分できない）場合というのは，実は世の中に多くある． たとえば， f(z) = z 2 は複素微分できないので非正則関数である． しかし， f(z) の実部と虚部がそれぞれ z = x iy の x や y で微分(2) f(x) = x2ニュートン法を用いても非線形方程式を解くことができますが、 一般的に二等分割法よりも解を得る収束が早いといわれています。 二等分割法のように求める解を挟まなくて良いので、 より柔軟な計算がおこなえます。 しかし、1部分で割り算を用いていることから、0除算，0に限りなく近い

 ニュートン法の実装 # (解を求める方程式, 初期値, 微分で用いる微小量, 許容(絶対)誤差, 反復の最大数) def newton_method (f, x0, h= 1e4, tol= 148e8, maxiter= 50) for cnt in range (1, maxiter 1) # 中心差分で微分を求める df = (f(x0 h) f(x0 h)) / (2 * h) next_x = x0 f(x0) / df # 反復回数, 解の近似値x, f(x)を表示 print ('{2d はじめに 『ゼロから作るDeep Learning 3』の初学者向け攻略ノートです。『ゼロつく3』の学習の補助となるように適宜解説を加えていきます。本と一緒に読んでください。 本で登場する数学的な内容をもう少し深堀りして解説していきます。 この記事は、主にステップ29「ニュートン法 数値微分 の手法としてよく知られている 二分法 と ニュートン法 の違いを説明します． 二分法は，解を含む区間の中間点を求める操作を繰り返すことで方程式を解く反復法による求根アルゴリズムです． 二分法は1次収束なので収束（Convergent）までが

書記が数学やるだけ 16 ニュートン法による近似 最適化のアルゴリズム 21 01 17追記 Malinka書記 Note

微分と積分 微分 科学雑誌newton 数学 Kindleストア Amazon

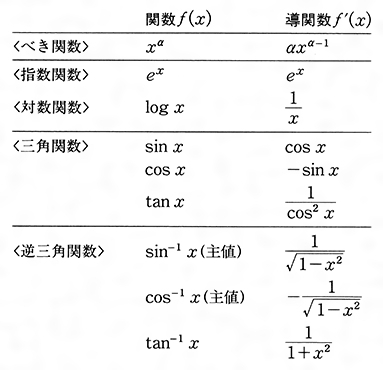
導関数 f ' (x)にX1を入れると f ' (X1)、X1の時の 「傾き(微分係数)」が出る。; ニュートン法とは、関数の解を近似的に求める手法の一つで、考え方としては、任意のx 1 におけるf(x 1 )の接線のx軸との交点x 2 は、x 1 よりf(x)=0の解に近くなるというものです。実例にて説明いたします。 ニュートン法 トップメニュー 数学 微分積分 ・微分公式 ・偏微分 ・数値微分ニュートンの記法（にゅーとんのきほう、英 Newton's notation ）は、数学における微分の記法のひとつである。 この記法はアイザック・ニュートンが fluxion （流率・流動率） と呼称した時間に対する変化率を表すために導入したもので、関数名の上部に微分の階数と同数のドット符号を記す。

ニュートン法の解説とそれを背景とする入試問題 高校数学の美しい物語

Newtonライト 微積のきほん ニュートンプレス

ニュートン 微分積分学 ライプニッツ 微分積分学 1．年表 シシリー島シラクサ アルキメデス (Archimedes) BC287 212 我に一つの支点を与えよ。さすれば地球を動かして見せよう。 ヘウレーカ！ 円周率の計算、円の面積、球の表面積 わが円を踏むな！ 2．古代ギリシャでは 3 10 71 < !世界大百科事典 第2版 微分積分法の用語解説 古く17世紀前半rデカルトの時代には，記号による算法を漠然と解析と呼んだ。それで17世紀後半にiニュートンとgwライプニッツの発見した微分積分法は，無限小の解析とも呼ばれた。現在では，無限に関する極限の概念をおもな対象とする数学 第67回 微分・積分の数学 ニュートン・ラフソン法 前編 09年9月24日 平田敦 数学, Java, 微分, 積分, ニュートン・ラフソン法, 関数 この記事を読むのに必要な時間：およそ 2 分 1 2 離れたところに飛んでくるテニスボールに対して， プレイヤーは先ず

微分と積分 改訂第２版 ニュートンプレス

ニュートン法とは サイエンスの人気 最新記事を集めました はてな

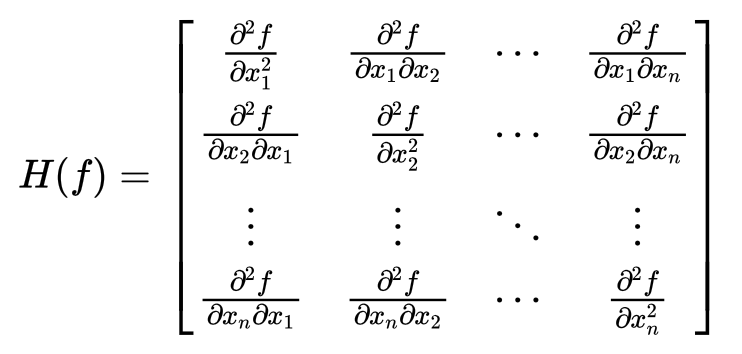
PART 2 ニュートンの微分法 接線の引き方 曲線上を動く点 瞬間の進行方向 微分法の誕生 微分で関数が生まれる PART 3 微分と積分の統一 アルキメデスの求積法 ケプラーの求積法 カヴァリエリの原理 Column 7 積分を発展させたガリレオの弟子たち Column 8 「 カヴァリエリの原理」を使ってみよう 準ニュートン法では目的関数の1階微分までしか使わない。そのなかでもbfgs公式による準ニュートン法では反復ごとに最大 \(n^2\) の計算で済む。 bfgs公式による準ニュートン法 準ニュートン法ではヘッセ行列を逐次計算によって近似したものをつかう。(1) f(x) = x2 2!!

ヤガミ 微分方程式 より ニュートンラプソン法 数値解析 微分方程式 Differentialequation 常微分方程式 Ordinarydifferentialequation 数値解析 Numericalanalysis Newtonraphsonmethod T Co Gfhmz1mnrp

微分積分 運動を語る数学の共通言語 空間情報クラブ 株式会社インフォマティクス

 微分法の発見だ。1666 年 10 月、ニュートンによる。 では、微分の逆はどうだろうか。 1669 年にニュートンは、曲線の"下"の部分の面積、すなわち、曲線と x 軸に囲まれた面積を求める3つの規則を与えた。その内の「規則1」を見ておこう。規則1は 微分を並べるだけです。ちなみに、一変数の場合は次のようになります。 ニュートン法について ではニュートン法ですが、まず正定値行列を知る必要があります。正定値行列とは 行列 が正定値とは、 に対して となること。ニュートン法の定義と収束するための条件および速度について分かり易く解説しています。よろしければご覧ください。 理数アラカルト ニュートン法とは？ ～定義と性質～ 目次 定義 具体例 速度 二次収束 収束条件 定義 ニュートン法とは、方程式 の解を数値的に求める方法の一つ

Humanoid K S Diary

Kj7

 ニュートン法とは ニュートン法はある方程式f(x) = 0の実数解を求めるための方法です。例えば$ f(x) = x ^ 3 2 $ にすると$ \sqrt3{2} $の値を知ることができます。微分を少し使います。 概要 全体的な流れは次のような感じです 1 初期値$ x_0 $の設定 2 $ n = 0 $とニュートン法 岡山大学工学部情報系学科 後藤佑介 工学基礎実験実習 前回までのまとめ C言語の基礎を学習 変数と定数 算術 制御の流れ 基本的な入出力 関数 LaTeXによるレポート作成，提出 数値計算方法であるNewton 法を例にして学習 2 工学基礎実験実習 今日やること ニュートン法のニュートン Newton， Sir Charles Thomas 生 ヘレフォード，ブレドワーダイン 没 ケント，マーゲイト イギリスの考古学者。オックスフォード大学を卒業後，1840年に大英博物館の考古学室の助手となったが，52年に辞任し，小アジア地方の調査を目的に，レスボス島のミティリニに副

メルカリ ニュートン 別冊 ニュートンの大発明 微分と積分 参考書 1 0 中古や未使用のフリマ

ニュートン式 超図解 最強に面白い 微分積分 Amazon Com Books

せていただくことになる減衰最小二乗法などの構造もそこから理解しやすくな る。 1． 1次元の場合のニュートン－ラフソン法の応用 関数f(x)が、1回微分f'(x)のみならず2回微分f''(x)が可能なものである 場合、前回の勾配法よりも効率の良い最適化手法と微分積分は、ニュートン力学を証明する手段として誕生したといっても過言ではありません。 それくらいに、物理学や力学に密接に関係したものなのでした。 微分積分を簡単に言いますと、その方法は先述したデカルトの四つの法則の中の二番目と三番目に当たります。 二番目は、複雑なもの< 3 1 7 3 á

Quasi Newton Method

数理最適化の勉強メモ 最急降下法 ニュートン法の原理と特徴 かみのメモ

 ニュートン法の導出 f (x)の微分すると導関数の f ' (x)が出る;ニュートン法が二次収束することが示されたから である．さらに，相補性問題に対しこれらを適用し た場合，従来からの微分可能なアプローチよりも， 効率的に解を求められることがわかってきたから である4, 5．ここでは，セミスムーズニュートン 法の理論と，相補性問題に対する応用にニュートン方程式 十河 清 1 力学を学ぶ―私の経験から も同様で，微分法の性質（積の微分と合成関数の 微分）だけを使っており，具体的に微分を実行し ているわけではないからである。 そういう事情から，『力学i』では，力学と微分積 分を平行して導入することを主たる目標とし

微分積分学の歴史 理系のための備忘録

微積分が導いた宇宙の法則 万有引力の発見は数学の賜物 サイエンス テクノロジー 研究 社会連携 京都産業大学

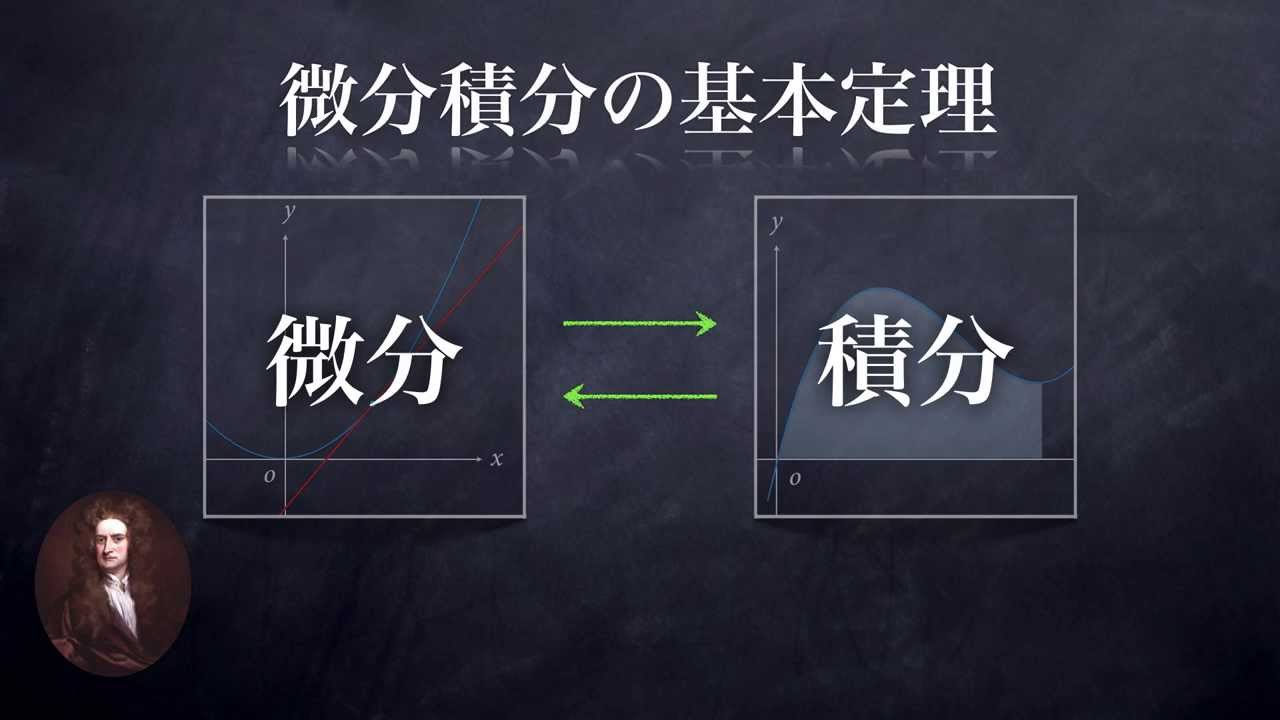
微分係数と傾きの定義の関係を利用して導出します。 @see 優技録 分数の式変形 漸化式が出来た。 これをループさせていくと目的の解に限りなく近く関数を微分するとみえてくる「法則」とは？ 微分すると，「変化のようす」がわかる！ 高校の数学で教わる接線の引き方は？ 微分で使う記号や計算のルールをニュートンの微積分法– p4/15 曲線の下の面積 以上より 1 は の原始関数であり 2一般に は の原始関数である： 従って、微積分法の基本定理より とすると最初の公式が得られる。 ニュートンの微積分法– p5/15 曲線の下の面積 以上より 1 cn mn xmn n はcx m n の原始関数であり ニュートンの微

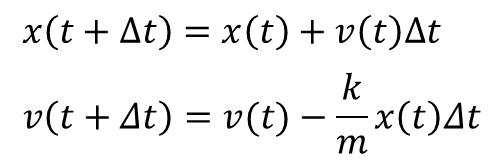
Step 05 ２階常微分方程式を解いてみる ニュートン方程式 筑波大学原子核理論研究室

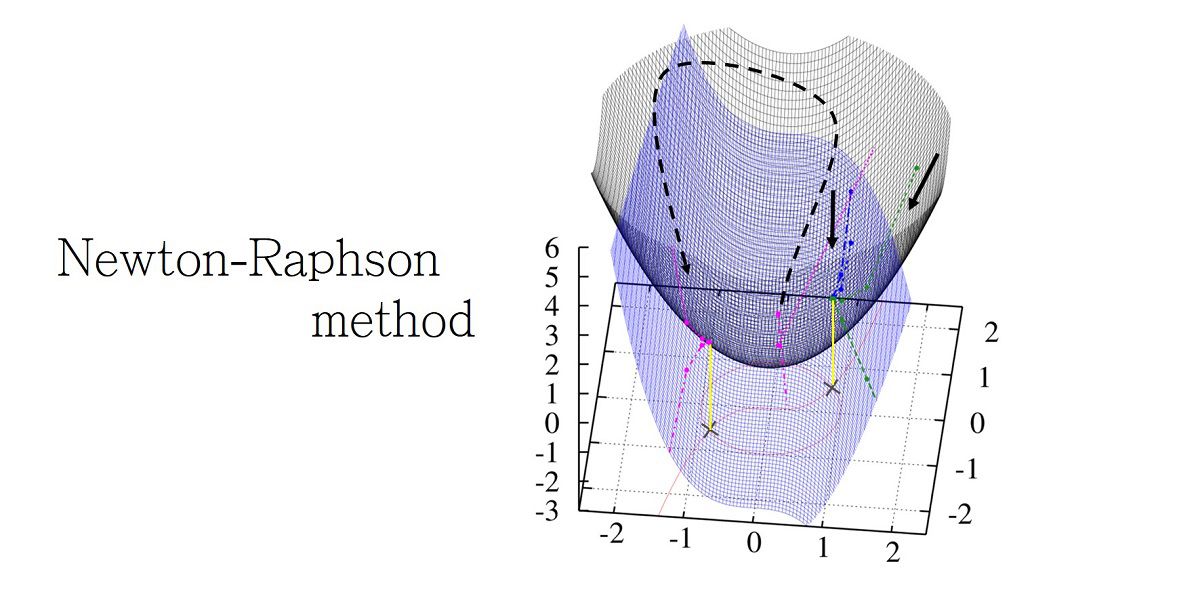
ニュートン法 1 2次元 多次元 シキノート

 少し前には、\(f(x)=0\) の解を2分法により求める C アルゴリズムについて紹介しました。 C 非線形方程式の解法（2分法）！今日は、方程式 \(f(x)=0\) の解をニュートン法により求める C アルゴリズム についてです。ニュートン法の概念・アルゴリズムは以下の通り。ライプニッツとニュートン：微積分学発⾒の優先権論争 ライプニッツが微分法の研究に打ち込んだのは、パリに滞在していた1675年から76年に かけてである。 ライプニッツよりも10年ほど前に、ニュートンが⼒学的な観点から微分法を発⾒していた。 ニュートン法の欠点としては、初期値の与え方によっては、収束しない場合もあり、常に解が求められる保証はないという点があげられます。 ここでは、ニュートン法の考え方、アルゴリズムとサンプルプログラムを記載します。 ニュートン法による非線形方程式の解法 ニュートン法は、

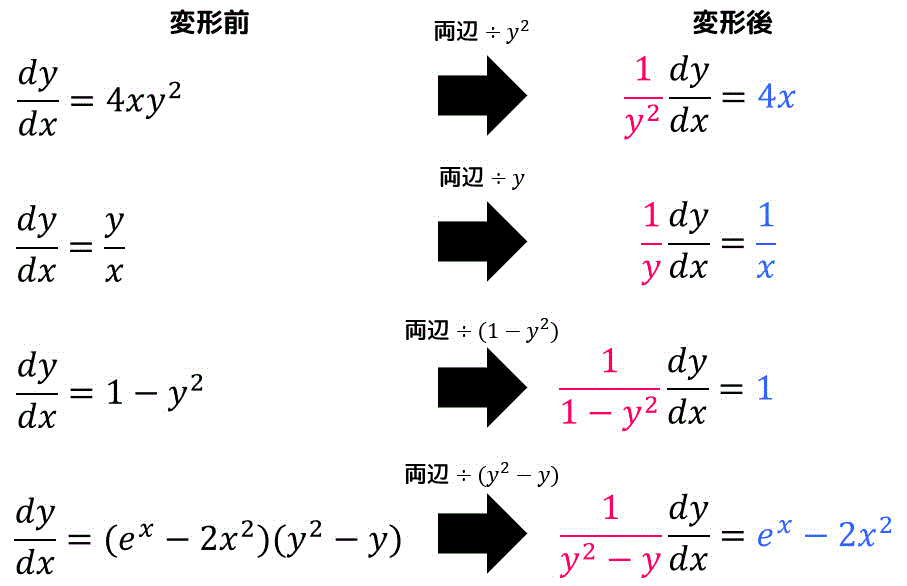
うさぎでもわかる微分方程式 Part01 変数分離形 1階微分方程式 工業大学生ももやまのうさぎ塾

Mer ニュートンは微積分学 Calculus をつくり 結石 同じく英語でcalulus で亡くなったのでした Newton別冊 微分と積分 新装版 より そ それは知らなかった というかnewton この別冊シリーズは初めて読みましたが 良いですね 全て揃えたく

ニュートン法 連立一次方程式の解法 ガウス・ジョルダン法 ガウス法 lu 分解ヤコビ法ガウス・ザイデル法 関数近似と補間法 最小二乗近似 ラグランジェの補間法 ニュートン前進補間公式 数値積分法 区分求積法 ニュートン・コーツ法 台形公式シンプソン公式ガウスの数値 積分公式 一階常微分 当時はまだ微分法は､まともな数学とは見なされていなかったからだ。 そこで ライプニッツは､これらの考え方を体系化し､ 微分積分学を厳密な学問 として確立 させた。お陰で当時は､ "ニュートンの盗作だ" と非難された。

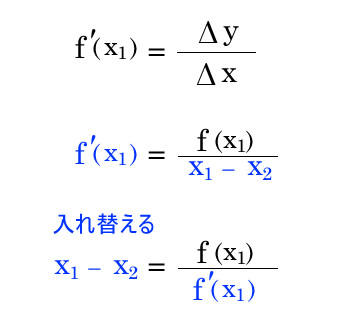
ニュートン法で近似解 Python Numpy 優技録

微分法とは コトバンク

3

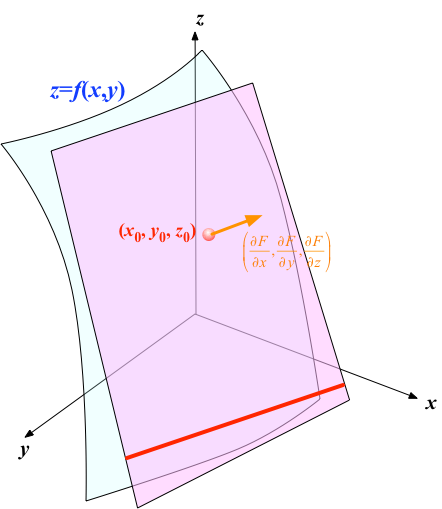
情報基礎 Pythonプログラミング ステップ７ 多変数のニュートン法

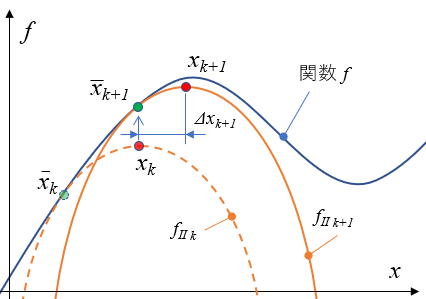
ニュートン法はどのように収束していくのか 1変数の場合で視覚化 仕事と投資とあと何か

ライプニッツとニュートン なぜ差がついたか それは 記号 だ 佐藤 恒雄 ブルーバックス 講談社 1 2

微分法や流率法はニュートンが考案したそうですが 現在では普通の学者で Yahoo 知恵袋

楽天ブックス Newton ニュートン 増刊 微分と積分 19年 08月号 雑誌 ニュートンプレス 雑誌

アフィン共変ニュートン法 Wolfram言語 12の新機能

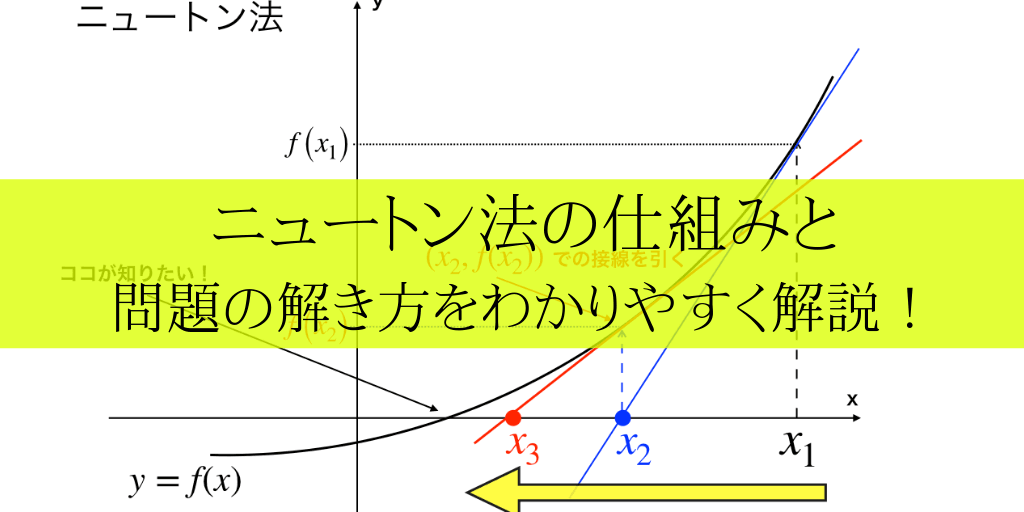
ニュートン法の仕組みと証明の仕方を分かりやすく解説

カオス２ ベクトル場 Chaos

微分積分学 Wikipedia

微分 微分の表記 ラグランジュ記法とライプニッツ記法 大人が学び直す数学

微分積分 これなら よくわかる の通販 紙の本 Honto本の通販ストア

微分導入時の雑談 怜悧玲瓏 高校数学を天空から俯瞰する

ニュートン法の仕組みと証明の仕方を分かりやすく解説

微分積分 運動を語る数学の共通言語 空間情報クラブ 株式会社インフォマティクス

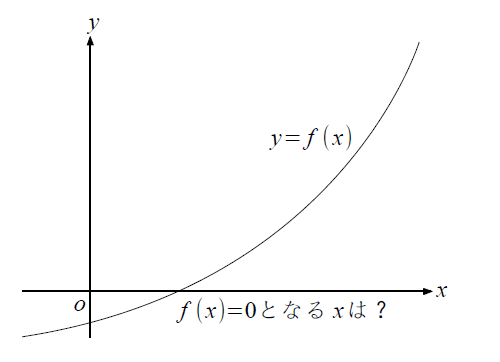
ニュートン法 ゆるゆるプログラミング

C言語でニュートン法を実装してみた Qiita

ニュートン法 Miidas Research

プログラミング 解けない方程式を解きたい 数値解析 ニュートン法 りけいのり

ニュートン法とは 制御工学の基礎あれこれ

森本 S Site On Strikingly

高校数学 ニュートン法 F X 0の実数解と累乗根の近似値 受験の月

ニュートンの大発見 微分と積分は逆関係 Youtube

文系のためのめっちゃやさしい微分積分 山本 昌宏 監修 紀伊國屋書店ウェブストア オンライン書店 本 雑誌の通販 電子書籍ストア

ニュートン法による求根 Thoth Children

微分積分 基礎

C言語 ニュートン法のプログラムの為の数値微分 Visual Studioでc C言語 C C 教えて Goo

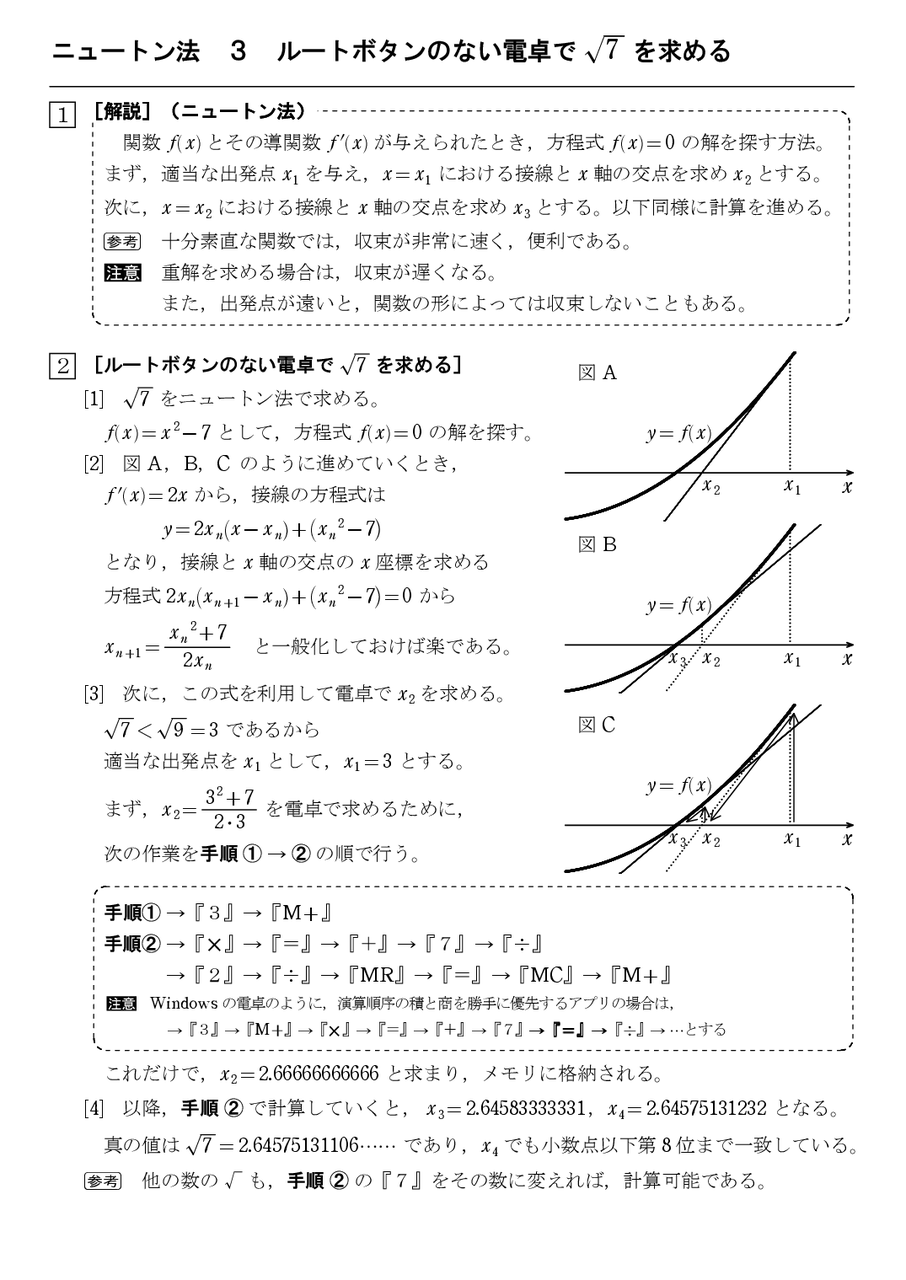
ニュートン法 ３ ルートボタンのない電卓で平方根を求める 怜悧玲瓏 高校数学を天空から俯瞰する

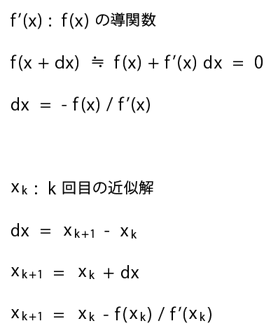
37 Newton 法 １ ２ Shade Labo 開発フォーラム Shade3d フォーラム

Berkley のnewtonのfluxionとleibnitzのdifference批判との比較 北村 正直 Ppt Download

万有引力 ニュートン

科学雑誌ニュートン年12月号 ゼロと微分積分 ニュートンプレス

Rpubs Com

最適化問題の基礎 ニュートン法とヘッセ行列 理系のための備忘録

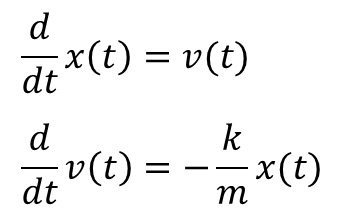
Step 05 ２階常微分方程式を解いてみる ニュートン方程式 筑波大学原子核理論研究室

楽天ブックス ニュートン式 超図解 最強に面白い 微分積分 高橋秀裕 本

ニュートン法 Wikipedia

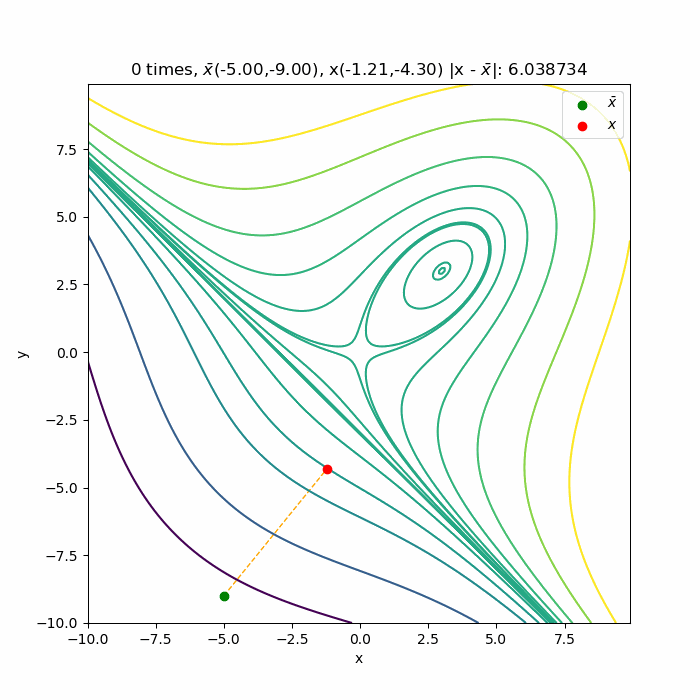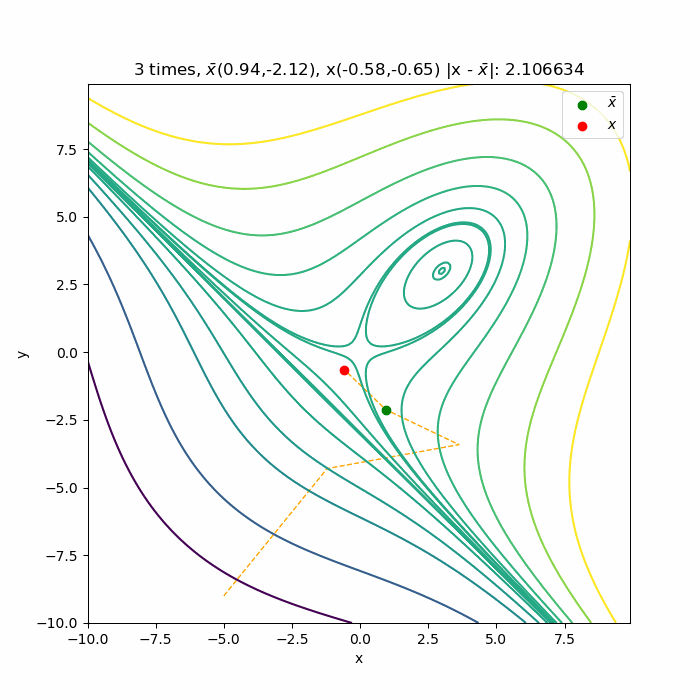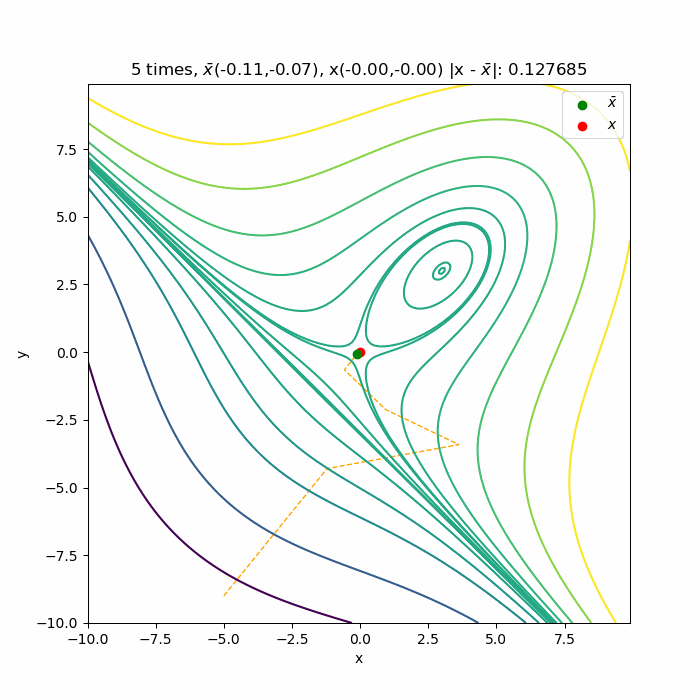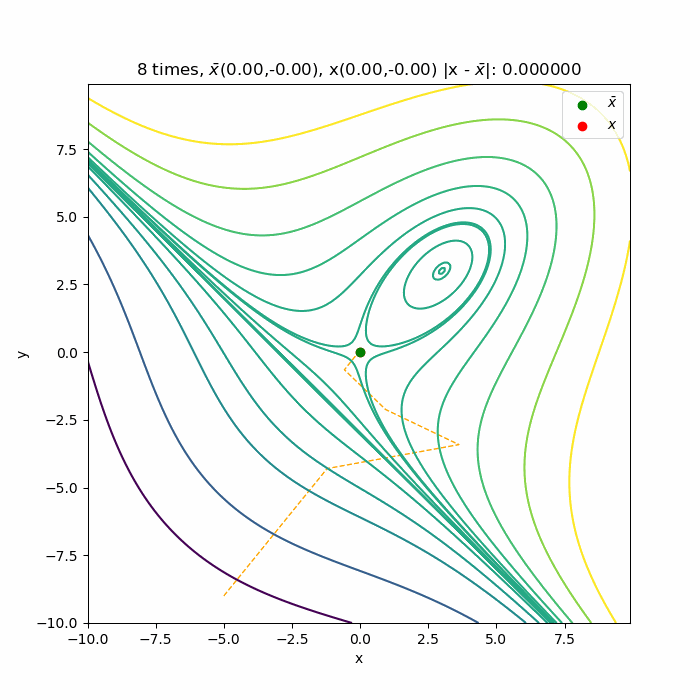
多変数のニュートン法の収束の様子を可視化 仕事と投資とあと何か

Glim Re Repo Nii Ac Jp

No 6 微分と積分 増補改訂版 ニュートンムック Ehomahouse

Newton法

Newton別冊 微分と積分 新装版 ニュートン別冊 本 通販 Amazon

ニュートン ラフソン法

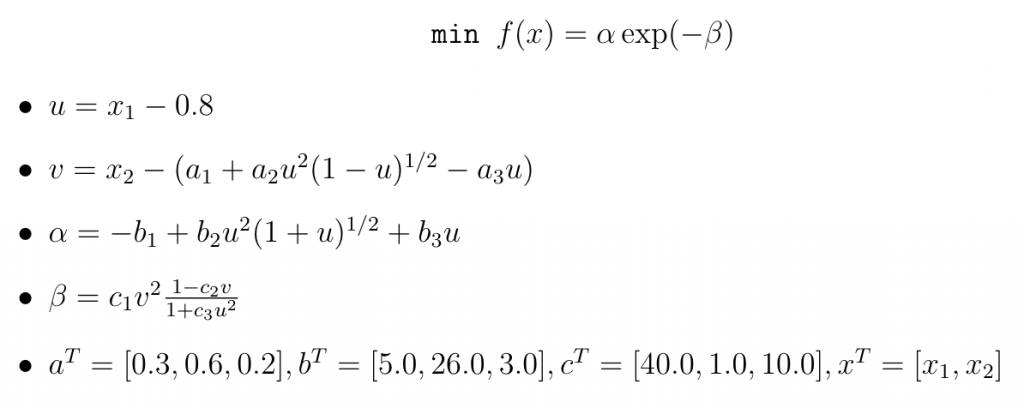
ニュートン法 Miidas Research

ロイロノート スクール サポートページ 高2 数学 微分法と積分法 数学 の微分法 の学習における反転授業の試みについて 実践事例 愛知県立熱田高等学校

メルカリ ニュートン 別冊 ニュートンの大発明 微分と積分 参考書 1 0 中古や未使用のフリマ

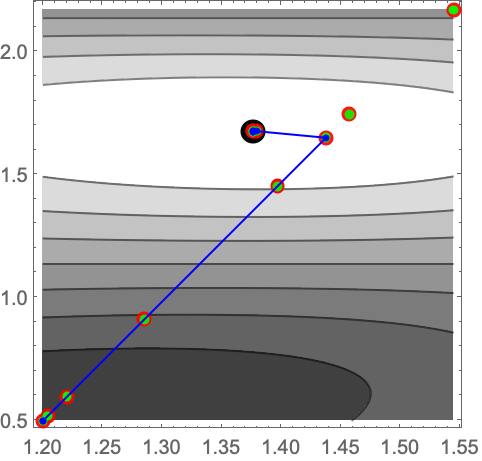
制約条件のない最適化 局所的最小化の方法 Wolfram言語ドキュメント

微分の表記法にはニュートン表記やライプニッツ表示などがありますが 微分の Yahoo 知恵袋

セカント法による求根 Thoth Children

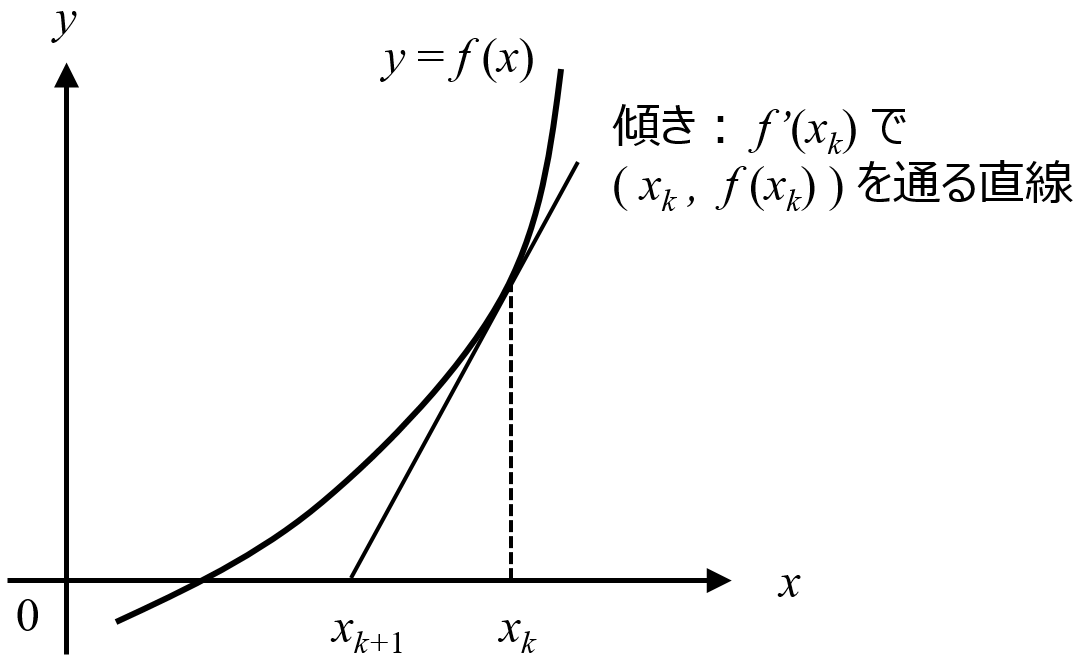
ニュートン法 ニュートン ラフソン法 F X 0の解を数値的に求める

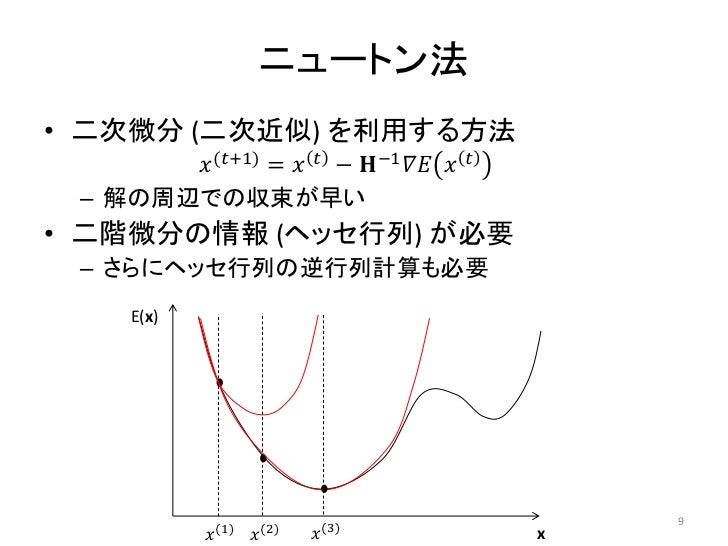
Cvim 11 3 最小化のための数値計算

Q ビセキブン とは何のことですか A 魔法です

R Source

ニュートンの知られざるダークサイド2 闘争編 アザミン Note

ニュートン りんご

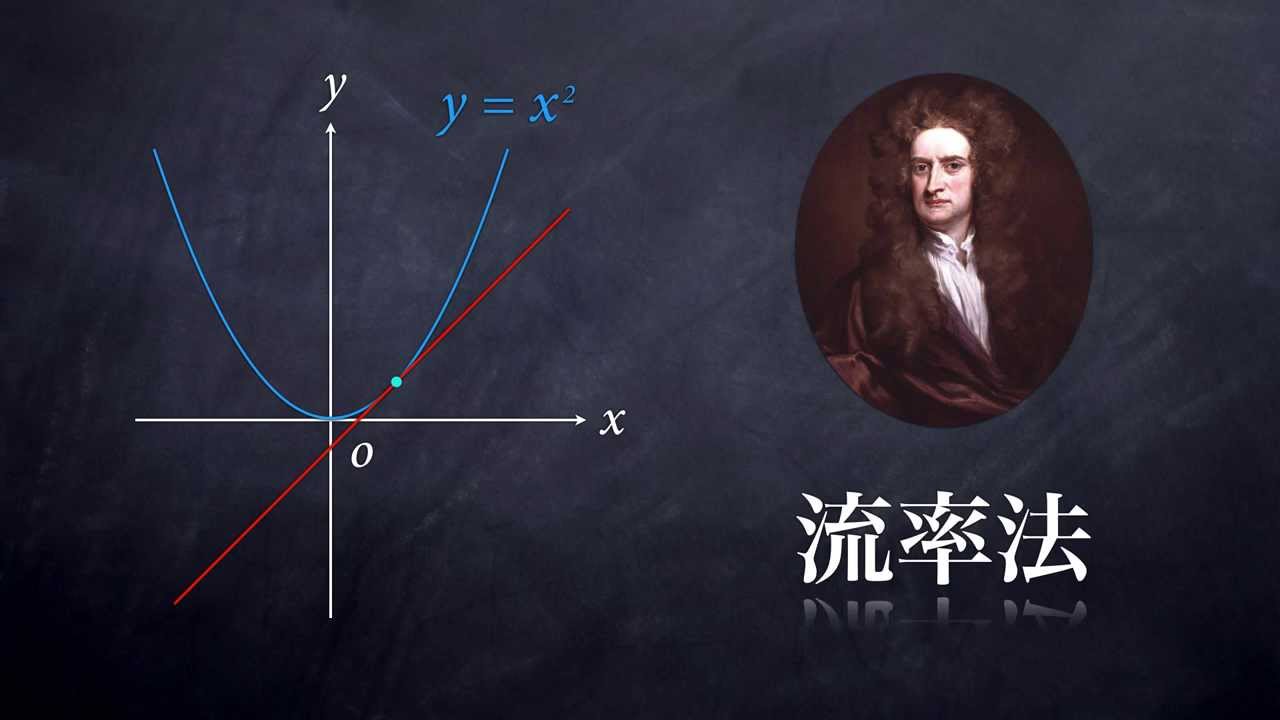
微分法の誕生 ニュートンの流率法 Youtube

Ocamlでニュートン法 1 微分の計算 I Am Bad At Math

筑摩書房 私の微分積分法 解析入門 吉田 耕作 著

微分 プログラマなら知っておきたいニュートン近似法 コンピュータの計算方法 偏差値40プログラマー

ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する

Nekodamashi Math Blog Ss Blog Jp

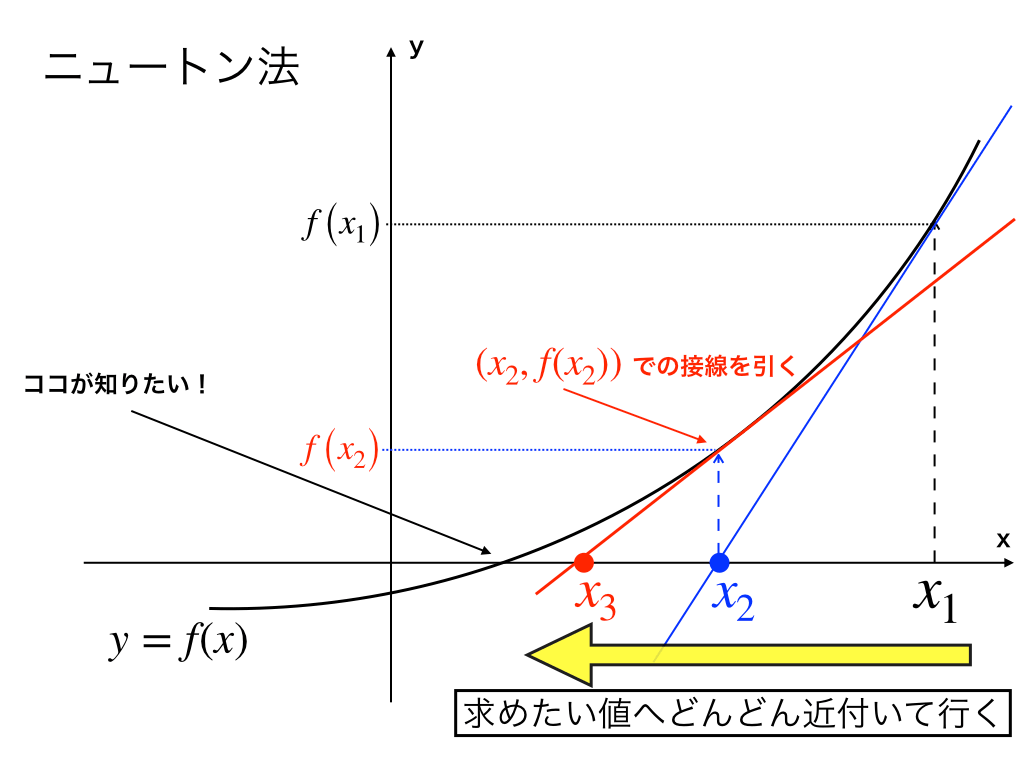
ニュートン法の仕組みと証明の仕方を分かりやすく解説

微分と積分 ニュートンの大発明 これならわかるの通販 紙の本 Honto本の通販ストア

微分積分法 を発見した学者が実は二人いた リンゴで有名な物理学者 ともう一人は ナゾロジー

ニュートン力学と微分方程式の意味がわかる 漫画 無料試し読みなら 電子書籍ストア ブックライブ

ニュートン法 数値計算 Youtube

ニュートン法とは 制御工学の基礎あれこれ

Newton Method For Stochastic Differential Equations From A Heuristic Algorithm Formulation To The Second Order Convergence By Kazuo Amano

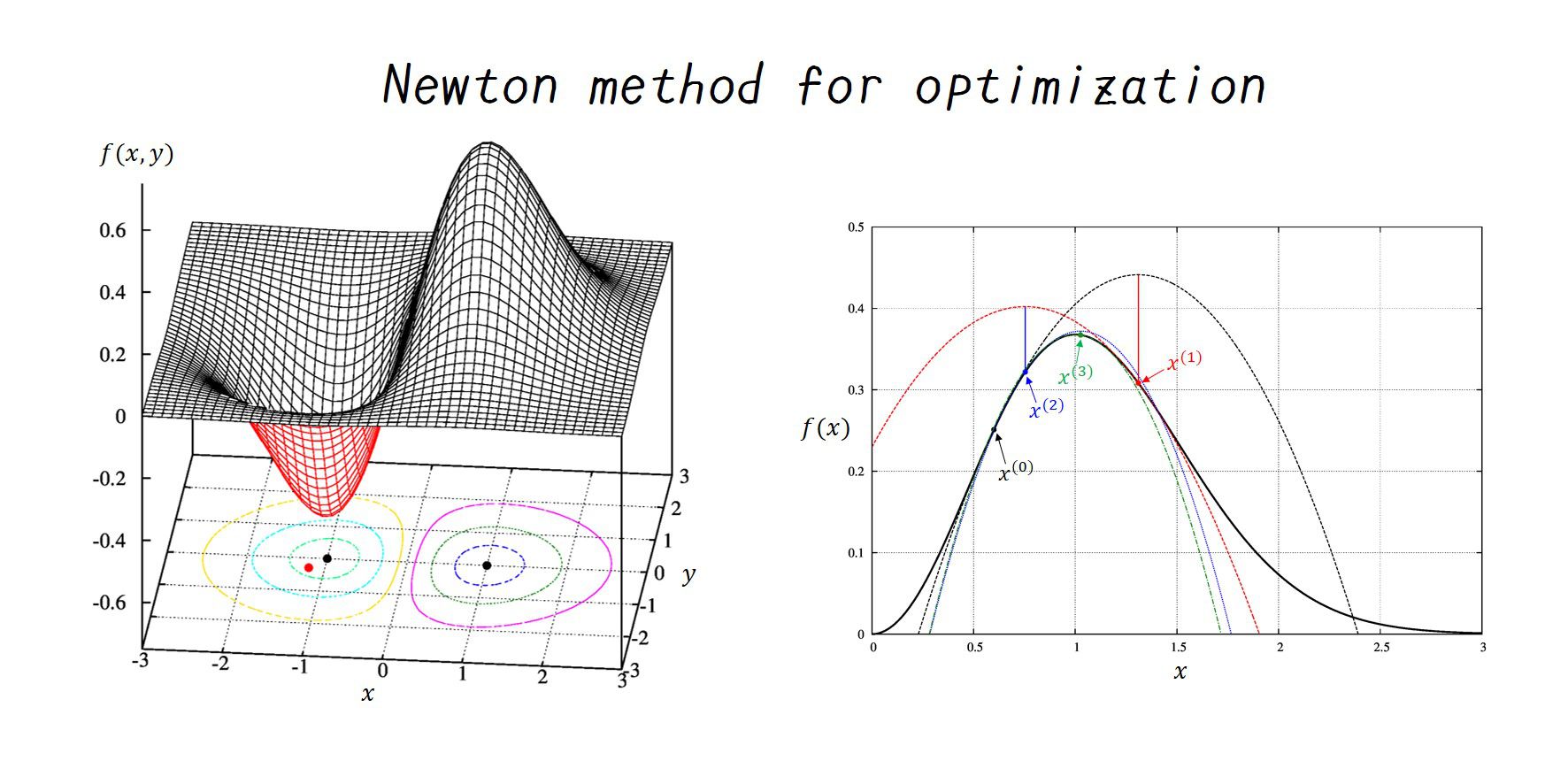
極値を求めるニュートン法 シキノート

Q ビセキブン とは何のことですか A 魔法です

ニュートンとライプニッツの微分積分 離散と連続から考える 書籍案内 技術評論社

微分積分を速度と距離の関係で理解する 自然科学研究会２ 生活の中の数学 その２

一言で言えばbfgs 準ニュートン法の紹介

マクローリン展開

遂次近似法３ ニュートン法 演習 身勝手な主張

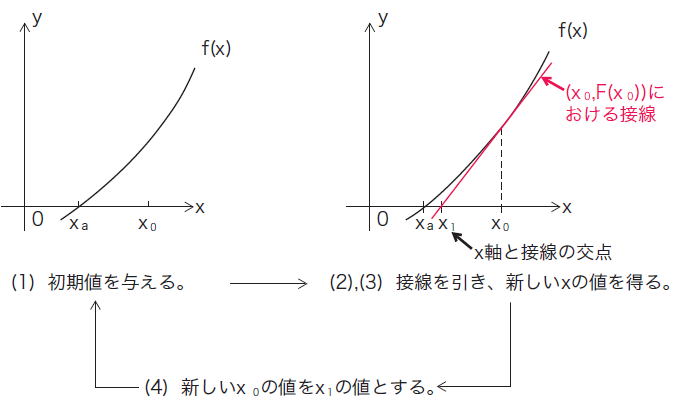
第67回 微分 積分の数学 ニュートン ラフソン法 前編 はじめmath Javaでコンピュータ数学 Gihyo Jp 技術評論社

ニュートン法とは何か ニュートン法で解く方程式の近似解 Qiita

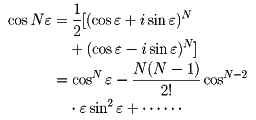
微分積分法とは コトバンク

微分積分入門 翻訳 ときどきブログ

No 6 微分と積分 増補改訂版 ニュートンムック Ehomahouse

Newton 年5月号 By 科学雑誌newton

Newton法

Incoming Term: ニュートン 微分法,